📝 Introduction
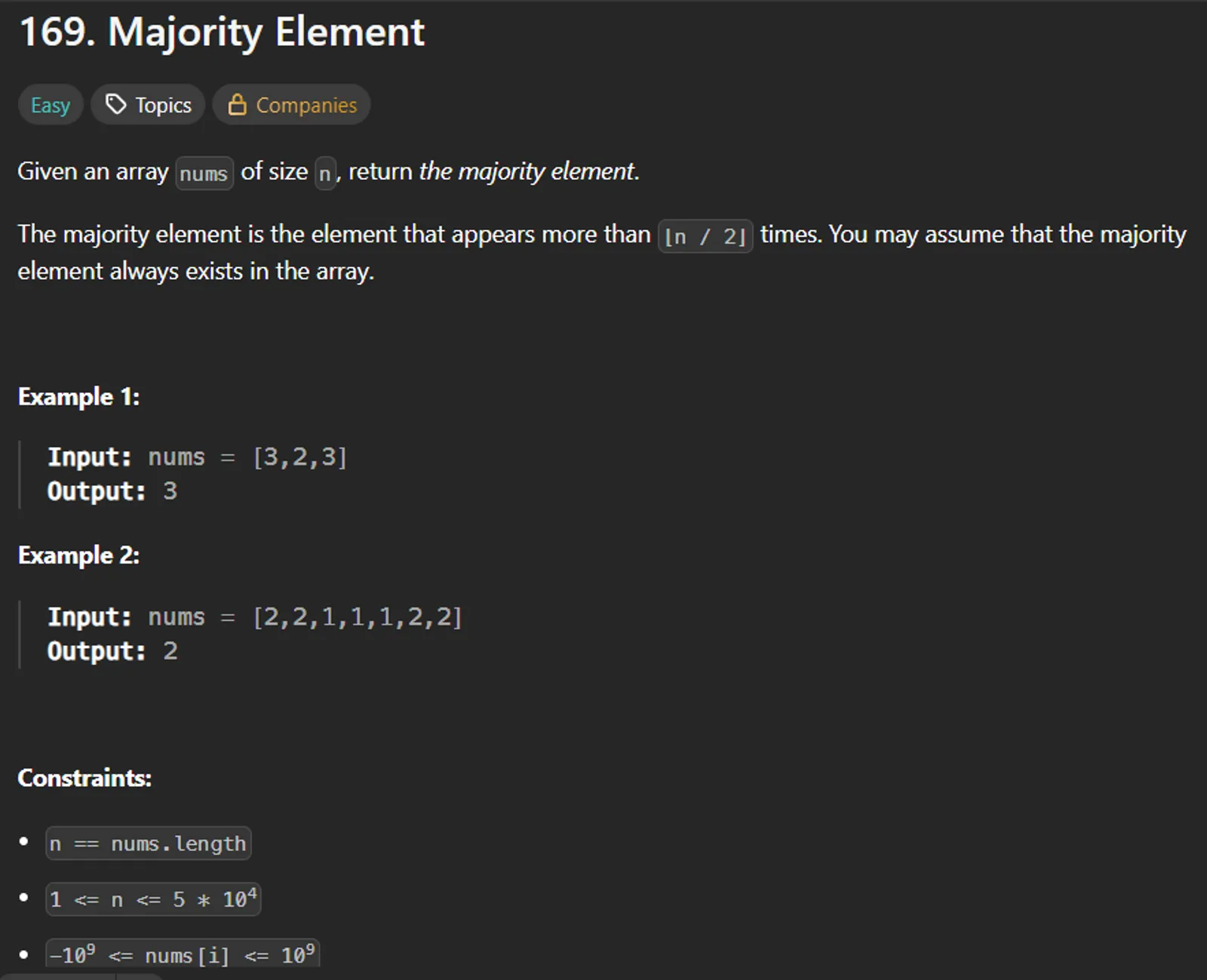
Given an array nums of size n, return the majority element — the element that appears more than ⌊n / 2⌋ times.
*Constraints typically include:
- It is guaranteed that the majority element always exists in the array.*
💡 Approach & Key Insights
*The problem centers on identifying an element that occurs more than n/2 times. Three approaches are commonly used:
- Brute-force with nested loops.
- Better approach using hash map frequency counting.
- Optimal approach using Moore’s Voting Algorithm for O(n) time and O(1) space.*
🛠️ Breakdown of Approaches
1️⃣ Brute Force / Naive Approach
- Explanation: For each element, count its frequency using a nested loop. If any element occurs more than ⌊n/2⌋ times, return it.
- Time Complexity: O(n²) – due to nested iterations.
- Space Complexity: O(1)
- Example/Dry Run:
Input: [3, 2, 3]Step 1: Check 3 → appears 2 times → not > 1.5Step 2: Check 2 → appears 1 time → not > 1.5Return 32️⃣ Better Approach
- Explanation: Use a hash map to store frequencies of each number. As you update counts, if any value exceeds ⌊n/2⌋, return it.
- Time Complexity: O(n) – single pass to count.
- Space Complexity: O(n) – for storing frequencies.
- Example/Dry Run:
Input: [2, 2, 1, 1, 1, 2, 2]Count Map:{2: 1}{2: 2}{2: 2, 1: 1}...{2: 4, 1: 3}Check: 4 > floor(7/2) = 3 → return 23️⃣ Optimal Approach
- Explanation: Use Moore’s Voting Algorithm. Keep a count and a candidate. If count is zero, pick a new candidate. If current number equals candidate, increment count. Else decrement. At the end, the candidate is the majority element.
- Time Complexity: O(n) – single pass.
- Space Complexity: O(1) – constant space.
- Example/Dry Run:
Input: [2, 2, 1, 1, 1, 2, 2]Step-by-step:candidate = 2, count = 12 == 2 → count = 21 != 2 → count = 11 != 2 → count = 0 → candidate = 1, count = 11 == 1 → count = 22 != 1 → count = 12 != 1 → count = 0 → candidate = 2, count = 1Final candidate = 2 → return 2📊 Complexity Analysis
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(n²) | O(1) |
| Hash Map Counting | O(n) | O(n) |
| Moore’s Voting Algo | O(n) | O(1) |
📉 Optimization Ideas
The Moore’s Voting Algorithm is already optimal, with a single pass and constant space. If the array does not guarantee a majority element, a second pass is needed to verify the candidate.
📌 Example Walkthroughs & Dry Runs
Example: [3, 3, 4, 2, 4, 4, 2, 4, 4]Step-by-step:candidate = 3, count = 13 == 3 → count = 24 != 3 → count = 12 != 3 → count = 0 → candidate = 2...Final candidate = 4 → verify by count = 5n = 9 → ⌊9/2⌋ = 4 → 5 > 4 → return 4🔗 Additional Resources
Author: Neha Amin
Date: 19/07/2025