📝 Introduction
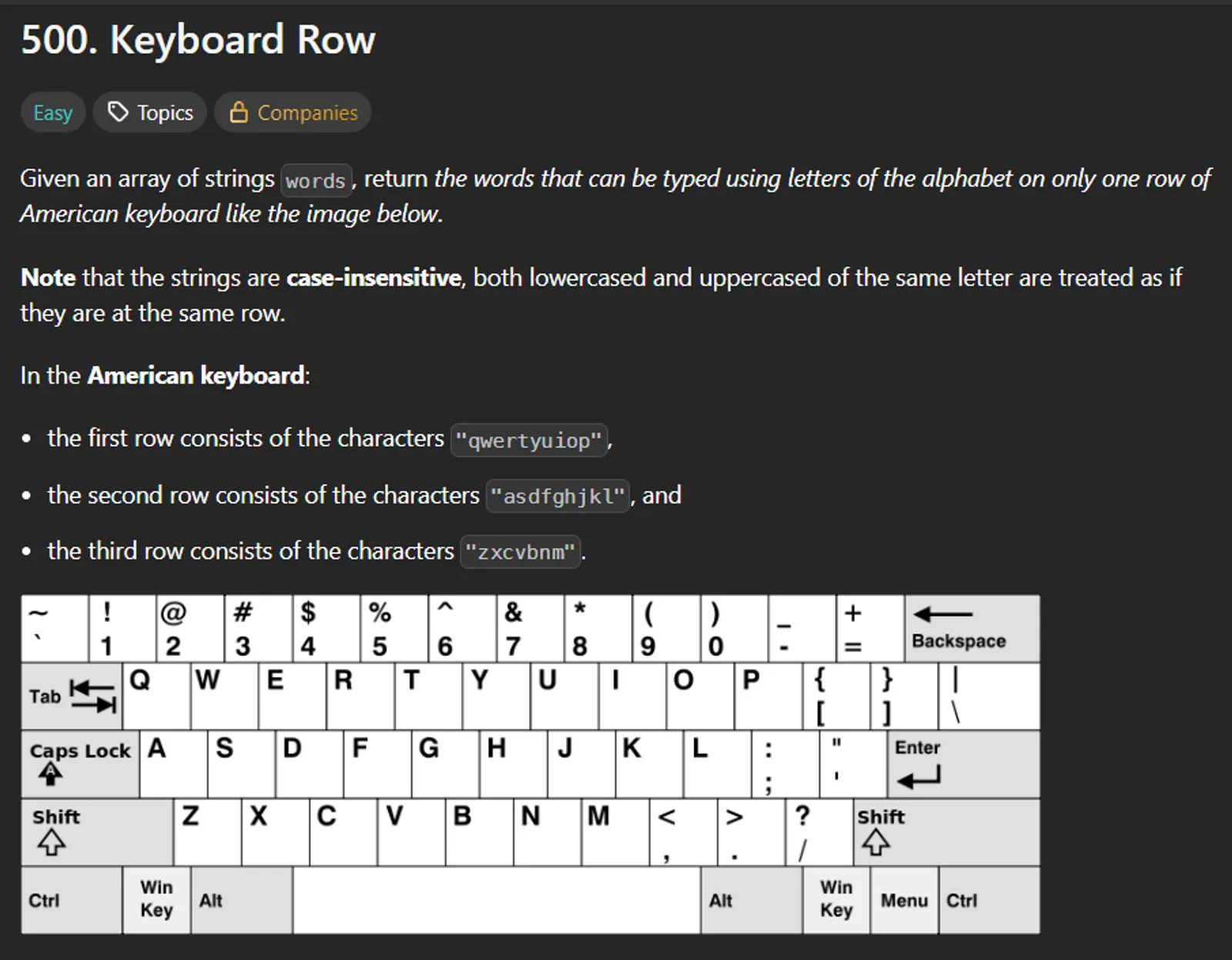
Given an array of strings, return the words that can be typed using letters of the alphabet on only one row of a standard American keyboard.
The keyboard rows are: Top row: qwertyuiop Middle row: asdfghjkl Bottom row: zxcvbnm
You may return the answer in any order.
💡 Approach & Key Insights
The main idea is to check for each word if all its characters belong to the same keyboard row. By converting each word to lowercase and then to a set, we can easily determine if its characters are a subset of any one row.
🛠️ Breakdown of Approaches
1️⃣ Brute Force / Naive Approach
- Explanation: For each word, check if every character belongs to the same keyboard row by comparing each character to the characters in all three rows. This involves checking character-by-character for each word.
- Time Complexity: O(n * m) - where n is the number of words and m is the average length of each word.
- Space Complexity: O(1) - ignoring output space.
- Example/Dry Run:
Example input: ["Hello", "Alaska", "Dad", "Peace"]
"Hello" → uses letters from multiple rows → ✘"Alaska" → only row 2 → ✔"Dad" → only row 2 → ✔"Peace" → multiple rows → ✘
Output: ["Alaska", "Dad"]2️⃣ Optimized Approach
- Explanation: Instead of checking characters one by one, convert each row into a set. Then convert the word into a lowercase set and check if it’s a subset of any of the three row sets.
- Time Complexity: O(n * m) - where n is the number of words and m is the average length of the words. Checking issubset is efficient for set comparisons.
- Space Complexity: O(1) - excluding the space for the output list.
- Example/Dry Run:
Example input: ["Hello", "Alaska", "Dad", "Peace"]
Step 1 → Convert keyboard rows into setsStep 2 → For each word, convert to lowercase setStep 3 → Check if set is subset of row1, row2, or row3
Output: ["Alaska", "Dad"]3️⃣ Best / Final Optimized Approach (if applicable)
- Explanation: The current solution is optimal for this problem. Using sets makes subset checking straightforward and efficient.
- Time Complexity: O(n * m)
- Space Complexity: O(1)
- Example/Dry Run:
Input: ["Type", "Row", "Zzz"]
"Type" → mixed rows → ✘"Row" → row 1 → ✔"Zzz" → row 3 → ✔
Output: ["Row", "Zzz"]📊 Complexity Analysis
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(n * m) | O(1) |
| Optimized | O(n * m) | O(1) |
| Best Approach | O(n * m) | O(1) |
📉 Optimization Ideas
You could pre-map each letter to its row number and then verify if all characters in a word belong to the same row number. This might slightly improve runtime in practice, but the set-based method is already clean and efficient.
📌 Example Walkthroughs & Dry Runs
Example:Input: ["Alaska", "Dad", "Peace"]
Process:1. Alaska → to lower → "alaska" → set("alaska") = {'a', 'l', 's', 'k'} ⊆ row2 → ✔2. Dad → "dad" → {'d', 'a'} ⊆ row2 → ✔3. Peace → "peace" → {'p', 'e', 'a', 'c'} ⊄ any row → ✘
Output: ["Alaska", "Dad"]🔗 Additional Resources
Author: Daniel Nallapalli Date: 16/06/2025