📝 Introduction
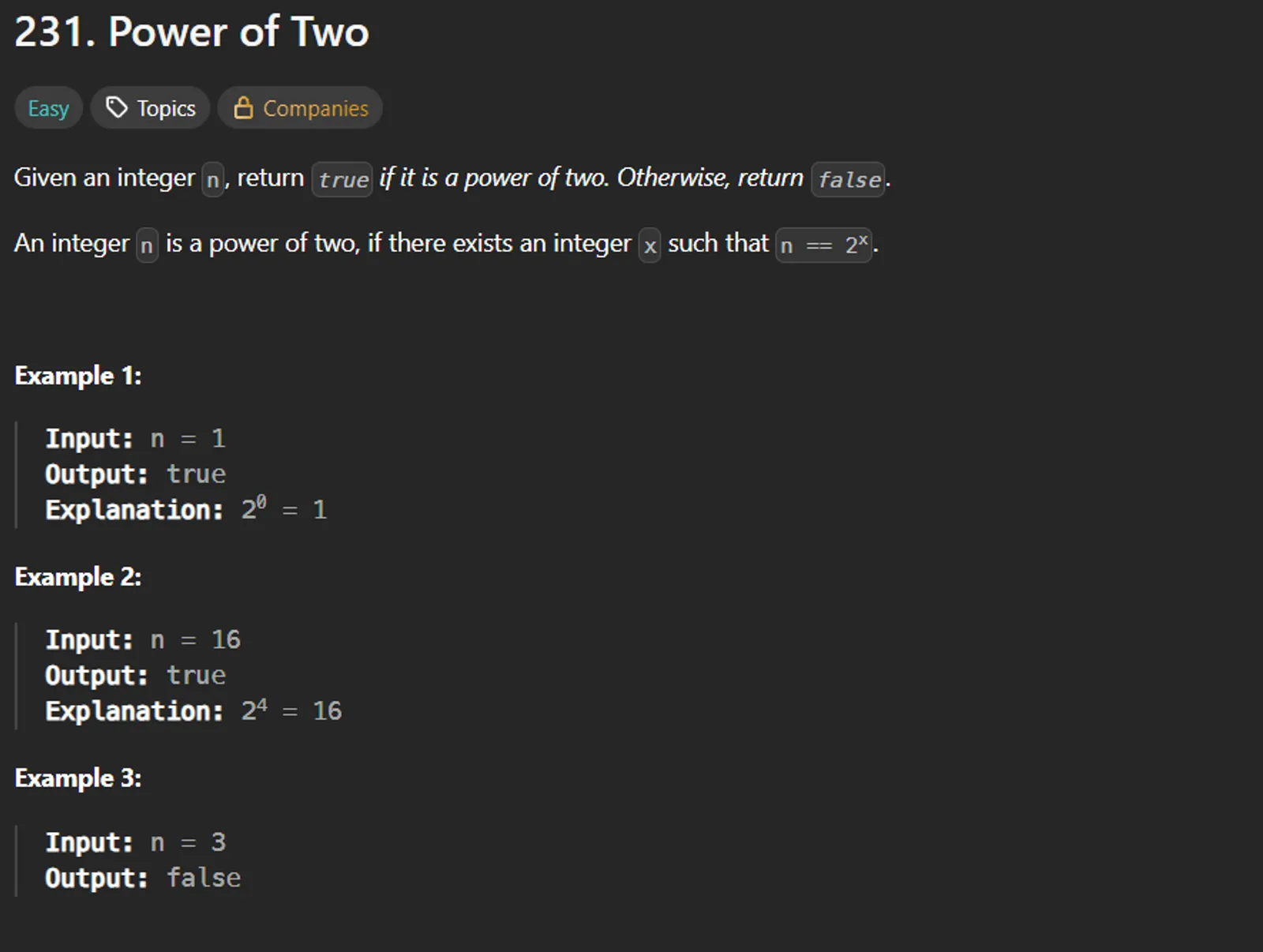
Given an integer n, return true if it is a power of two, otherwise return false.
An integer is a power of two if there exists an integer x such that n == 2^x.
Constraints:
-2^31 <= n <= 2^31 - 1
💡 Approach & Key Insights
Key Observation
A power of two in binary form has exactly one bit set to 1.
Examples:
- 1 →
0001 - 2 →
0010 - 4 →
0100 - 8 →
1000
For a number n that is a power of two:
n > 0(since negative numbers and zero cannot be powers of two)(n & (n - 1)) == 0(removes the only set bit, leaving 0)
🛠️ Breakdown of Approaches
1️⃣ Brute Force / Naive Approach
- Explanation:
Keep dividingnby 2 while it is even. If the result becomes 1, then it’s a power of two. - Time Complexity: O(log n)
- Space Complexity: O(1)
Example:
n = 16 → 16 → 8 → 4 → 2 → 1 → return true
2️⃣ Best / Optimized Approach (Bit Manipulation)
- Explanation:
For powers of two,(n & (n - 1)) == 0andn > 0. - Time Complexity: O(1)
- Space Complexity: O(1)
Example:
n = 8 (1000) n-1 = 7 (0111) n & (n-1) = 0 → Power of two
📊 Complexity Analysis
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(log n) | O(1) |
| Bitwise Check | O(1) | O(1) |
📌 Example Walkthroughs & Dry Runs
Example 1:
Input: n = 16
Binary: 10000
n - 1 = 01111
n & (n - 1) = 0
Output: true
Example 2:
Input: n = 3 Binary: 11 n - 1 = 10 n & (n - 1) = 10 (non-zero) Output: false
🔗 Additional Resources
Author: Kailash Senthilkumar
Date: 09/08/2025