📝 Introduction
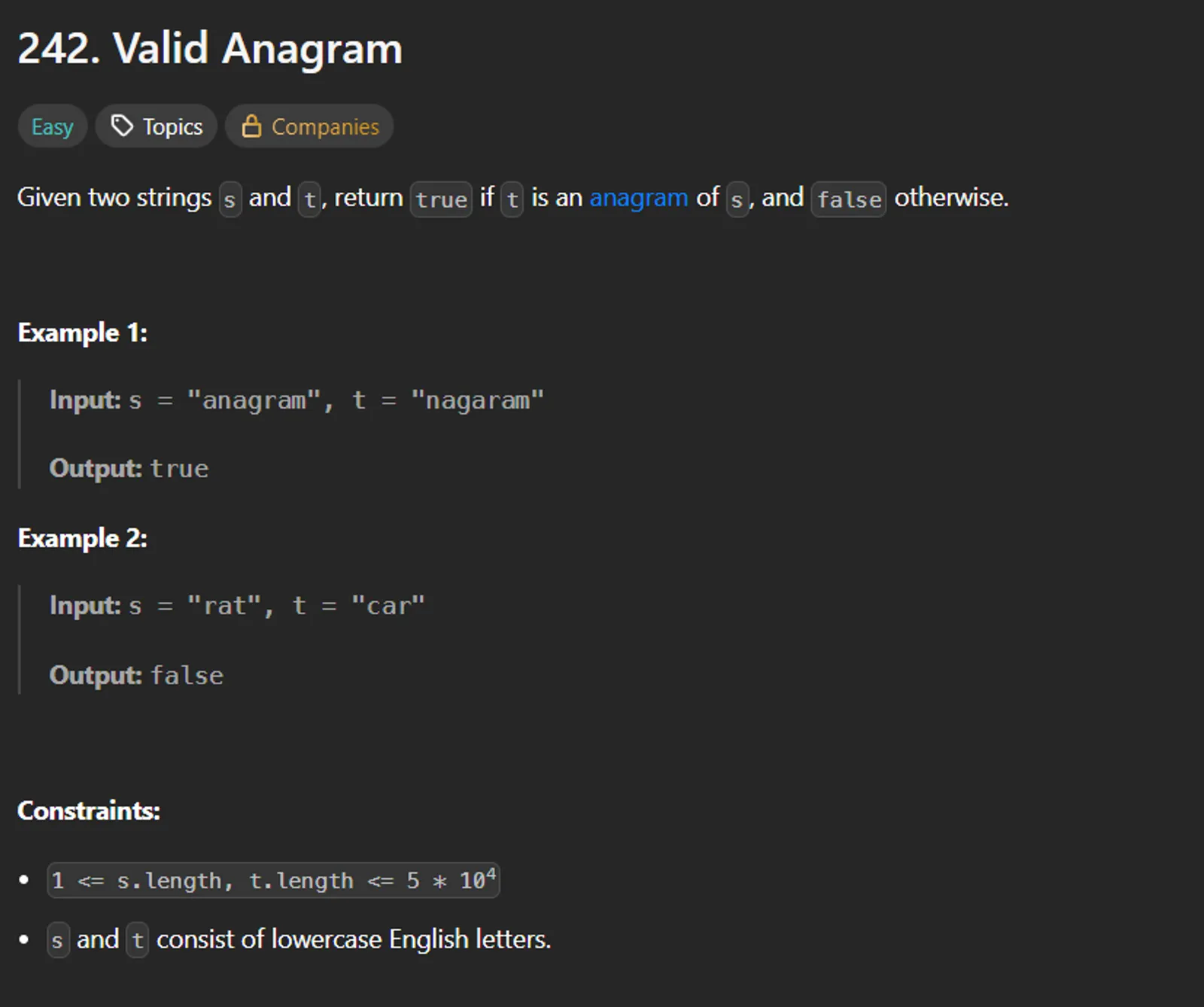
Given two strings, determine whether they are anagrams of each other.
Two strings are anagrams if they contain the same characters with the same frequencies, regardless of the order.
Constraints:
- Only uppercase letters (e.g., ‘A’ to ‘Z’) are considered.
- Strings must be the same length to qualify as anagrams.
- Output
trueif they are anagrams, otherwisefalse.
💡 Approach & Key Insights
- The core idea is to check whether the two strings contain the exact same characters with the same counts.
- If their lengths differ, they can’t be anagrams.
- There are multiple valid ways to compare character distributions:
- Sort and compare
- Count frequencies using a fixed-size array (best for character sets of known size)
🛠️ Breakdown of Approaches
1️⃣ Brute Force / Naive Approach — Sorting
-
Explanation:
Sort both strings and check if they are equal. If sorted versions are identical, then the strings are anagrams. -
Time Complexity: O(N log N) – Due to sorting of both strings.
-
Space Complexity: O(1) – Assuming in-place sorting.
-
Example/Dry Run:
Input: str1 = "INTEGER", str2 = "TEGERNI"Step 1: Sort str1 → "EEGINRT"Step 2: Sort str2 → "EEGINRT"Step 3: Compare both → Equal → return true
Output: true2️⃣ Optimized Approach — Frequency Count
-
Explanation:
Use a frequency array of size 26 (for uppercase letters).- Increment count for characters in str1
- Decrement for characters in str2
- If all frequencies are 0 in the end → anagrams
-
Time Complexity: O(N) – One pass for each string.
-
Space Complexity: O(1) – Fixed array size of 26.
-
Example/Dry Run:
Input: str1 = "INTEGER", str2 = "TEGERNI"Step 1: freq[] = [0,...,0]
Step 2: For str1 →I+1, N+1, T+1, E+1, G+1, E+1, R+1→ freq = {G:1, E:2, I:1, N:1, R:1, T:1}
Step 3: For str2 →T-1, E-1, G-1, E-1, R-1, N-1, I-1→ freq = all zero
Step 4: All frequencies are zero → return true
Output: true3️⃣ Best / Final Optimized Approach
-
Explanation:
Frequency counting is optimal for limited character sets (like uppercase/lowercase letters).- No sorting
- No additional data structures like maps or sets
- Linear time and constant space
-
Time Complexity: O(N)
-
Space Complexity: O(1)
📊 Complexity Analysis
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(N log N) | O(1) |
| Optimized | O(N) | O(1) |
| Best Approach | O(N) | O(1) |
📉 Optimization Ideas
- Convert both strings to the same case (e.g., uppercase) to make comparison case-insensitive if needed.
- If dealing with Unicode characters, use a
HashMapinstead of fixed-size array. - Early termination: While building the frequency array, if any count goes negative, return
falseearly.
📌 Example Walkthroughs & Dry Runs
Example 1:Input: str1 = "CAT", str2 = "ACT"
Step 1: freq[26] = {0}Step 2: +1 for C, A, T → freq[C]=1, A=1, T=1Step 3: -1 for A, C, T → all become 0Output: true
Example 2:Input: str1 = "RULES", str2 = "LESRT"
Step 1: freq[26] = {0}Step 2: +1 for R, U, L, E, S → freq[R]=1, U=1, L=1, E=1, S=1Step 3: -1 for L, E, S, R, T → freq[T]=-1 (unexpected char)Output: false🔗 Additional Resources
Author: Abdul Wahab
Date: 19/07/2025