📝 Introduction
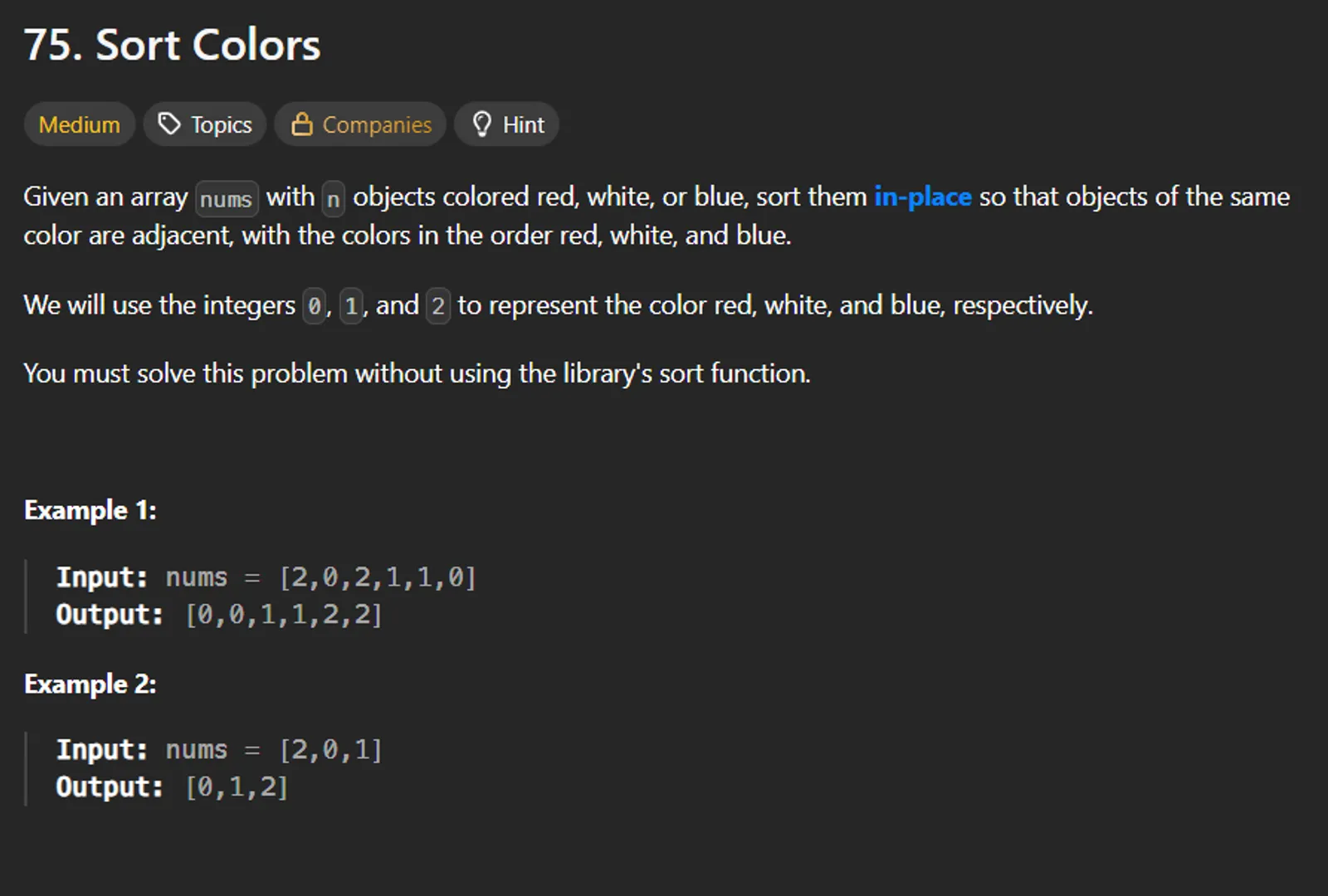
Given an array nums with n objects colored red (0), white (1), or blue (2), sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white, and blue.
*Constraints typically include:
- You must solve this problem without using the library’s sort function.
- The array contains only values 0, 1, and 2.*
💡 Approach & Key Insights
The problem can be solved through various approaches. Though sorting is a valid but not expected solution, we can explore better and optimal methods by leveraging the limited number of distinct values (0, 1, 2). This allows for more efficient counting or pointer-based techniques like the Dutch National Flag algorithm.
🛠️ Breakdown of Approaches
1️⃣ Brute Force / Naive Approach
- Explanation: Use the built-in sorting algorithm to sort the array. This works since the array contains only 0, 1, and 2, and sorting would naturally arrange them.
- Time Complexity: O(n log n) – standard sorting complexity.
- Space Complexity: O(1) – assuming in-place sort.
- Example/Dry Run:
Input: [2, 0, 2, 1, 1, 0]Sorted Output: [0, 0, 1, 1, 2, 2]2️⃣ Better Approach
- Explanation: Count the number of 0s, 1s, and 2s in one pass. Then overwrite the array in a second pass by placing the right number of 0s, 1s, and 2s.
- Time Complexity: O(n) – 2 passes through the array.
- Space Complexity: O(1) – constant space for counters.
- Example/Dry Run:
Input: [2, 0, 2, 1, 1, 0]Step 1: Count → count_0 = 2, count_1 = 2, count_2 = 2Step 2: Overwrite:[0, 0, 1, 1, 2, 2]3️⃣ Optimal Approach
- Explanation: Use the Dutch National Flag algorithm with three pointers (low, mid, high). Rearrange elements in a single pass.
- Time Complexity: O(n) – single pass.
- Space Complexity: O(1) – in-place.
- Example/Dry Run:
Input: [2, 0, 2, 1, 1, 0]Initial: low = 0, mid = 0, high = 5
Step-by-step:mid = 0, nums[mid] = 2 → swap(nums[mid], nums[high]) → high--mid = 0, nums[mid] = 0 → swap(nums[low], nums[mid]) → low++, mid++mid = 1, nums[mid] = 0 → swap(nums[low], nums[mid]) → low++, mid++mid = 2, nums[mid] = 2 → swap(nums[mid], nums[high]) → high--mid = 2, nums[mid] = 1 → mid++mid = 3, nums[mid] = 1 → mid++
Final Output: [0, 0, 1, 1, 2, 2]📊 Complexity Analysis
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(n log n) | O(1) |
| Counting | O(n) | O(1) |
| Dutch Flag (Optimal) | O(n) | O(1) |
📉 Optimization Ideas
The Dutch National Flag algorithm is already optimal — it solves the problem in a single traversal with constant space. No further optimization is necessary.
📌 Example Walkthroughs & Dry Runs
Example:Input: [2, 0, 1]Initial: low = 0, mid = 0, high = 2
1. nums[mid] = 2 → swap(nums[mid], nums[high]) → [1, 0, 2], high--2. nums[mid] = 1 → mid++3. nums[mid] = 0 → swap(nums[low], nums[mid]) → [0, 1, 2], low++, mid++
Output: [0, 1, 2]🔗 Additional Resources
Author: Neha Amin Date: 19/07/2025